"Если на клетке слона прочтёшь надпись «буйвол», не верь глазам своим."
Рост заболеваемости в начале эпидемии очень хорошо объясняется простой популяционной моделью Мальтуса y(x) = y0eαx. В данном случае постоянная роста α – это среднее число людей, заражённых одним инфицированным за один день. Эпидемия распространяется согласно модели, пока не проявятся обратные связи и эффекты насыщения, ограничивающие беспрепятственное распространение вируса.
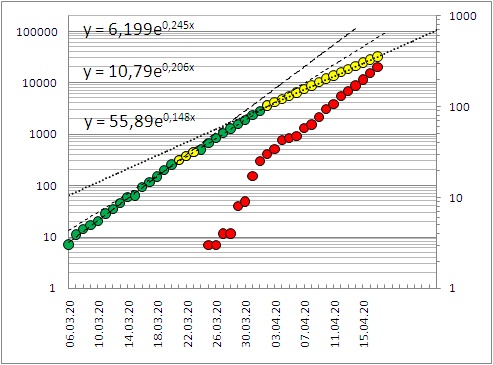◄ Полное число заразившихся коронавирусом в России
Значение α = 0.245 (на 20.03) означает, что число новых случаев заражения в день равно
0.245 полного числа заражённых: dy/dx = αy. Данные о заразившихся
(зелёные и жёлтые кружки) отражают динамику инфицирования с задержкой на
(медианный
инкубационный период 5.1 дней + время срабатывания системы) и дают всегда заниженную
оценку инфицированных, даже с учётом задержки. До 15.04 больше половины случаев приходилось на один
локальный регион – Москву, после – стала доминировать остальная страна.
Провалы на 15.03 и 22.03 коррелируют с
выходными. После 20.03 происходит слом тренда (жёлтым). Одновременно появляется
сообщение CNN (впервые упоминается
21.03 ): "... According to information released by Russian officials, Putin's strategy
seems to have worked ..." Это произошло до ввода 01.04 самоизоляции по стране.
После 02.04 тренд опять ломается. Тренды проведены по данным в интервалах
06.03-20.03, 21.03-02.04 и 02.04-. Их функциональный вид дан в соответствующем порядке.
Красным – число смертей.
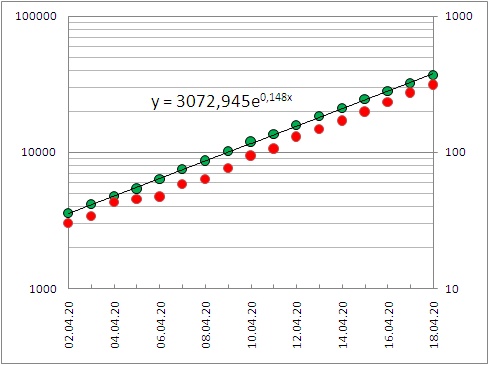◄ Полное число заразившихся коронавирусом в России со 2-го апреля
Разрыв коммуникаций в результате самоизоляции с 1-го апреля не отразился на росте
больных с симптомами коронавируса. Это означает, что или носителями вируса является
значительная часть населения, или возможные очаги распространения вируса не контролируются
самоизоляцией, например больницы и магазины. Здесь x = дата - 01.04.2020
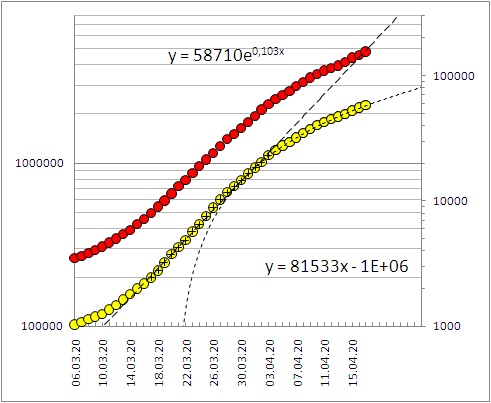◄ Полное число заразившихся коронавирусом в мире
Рост его в начале графика заметно круче экспоненциального закона, динамика процесса как бы
нелинейная. Именно, рост ускоряется, как если бы вирус становился более вирулентным.
Однако разнородность процессов (разная величина α) в регионах мира исключает простую
модель для их суммы. Слом тренда приходится на 11.03-17.03.
11.03 – ВОЗ объявила пандемию коронавируса. Постоянная роста α в мире на 26.03 была
примерно в 2.5 раза меньше, чем в России. На конце графика проявляется замедление
роста в сравнении с моделью беспрепятственного распространения инфекции.
Тренды проведены по данным в интервалах 07.03-03.04 и 04.04-.
Рост полного числа умерших от коронавируса в мире (красные кружки) следует
поведению числа заразившихся. В форме кривой не заметно
эффекта задержки на среднее время от заражения до смерти
17.3 дня, что вполне объясняется
неоднородностью данных по разным регионам.
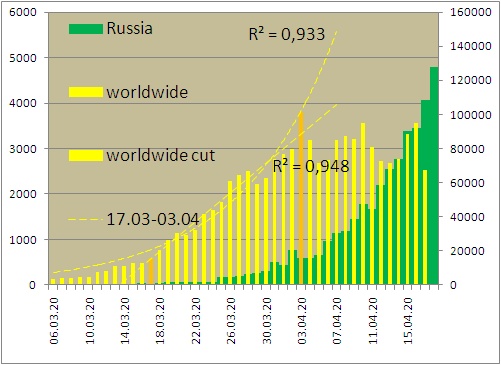◄ Скорость заражения коронавирусом в день в мире и в России
Показаны экспоненциальный и линейный мировые тренды на 17.03-03.04. Границы выбора данных для
трендов – оранжевые. Очевидно, что мировой рост сдерживается.
Функция зависимости числа случаев (y) от времени (x = дата - 05.03.2020) показана на графике. Её достоверность – R2. Кружки – данные Worldometer. Предсказание моделью числа заразившихся в России:
| Дата | Общее число | ||
|---|---|---|---|
| прогноз от 18.03 | прогноз от 16.04 | ||
| 31.03.2020 | 3398 | инфицирование до 18-24.03(эффект задержки) | |
| 12.04.2020 | 62004 | на окончание вынужденных школьных каникул | |
| 22.04.2020 | 697293 | 69718 | на голосование по Конституции |
| 24.04.2020 | 1131394 | 93922 | миллионный рубеж |
| 01.05.2020 | 266523 | 2 недели от 16.04 (максимальный период инкубации) |
В этой брошюре приводятся краткие сведения по общей физике в пределах университетского односеместрового курса. Каждый лист соответствует одной лекции − своего рода катехизис физики, или шпаргалка по физике с минимумом сведений, необходимым для сдачи экзамена по физике, а также для решения задач. Однако, материал шпаргалок не самодостаточен: связи, выводы и комментарии в них частично пропущены, пояснительные рисунки отсутствуют. Восполнить эти "пробелы" предлагается самому студенту во время лекции. Расположение текста шпаргалок оставляет место для собственных записей студента. Т.о. шпаргалки представляют собой каркас-схему, которая поможет студенту целиком "ухватить" лекцию в аудитории, с минимальными пропусками, и облегчит написание конспекта лекций.
Данное учебно-методическое пособие отражает опыт преподавания односеместрового курса общей физики в Тольяттинском государственном университете для студентов средних курсов. Предполагается, что студенты уже знакомы с математическим анализом, обыкновенными дифференциальными уравнениями и с теорией вероятности и статистики.
Данный курс читался студентам института химии в Тольяттинском государственном университете
Данный курс математической физики читался магистрам строительных специальностей. В силу ограничения курса всего 4 часами лекций и 18 часами практики он является вводным курсом по математической физике. Основным содержанием пособия являются классификация дифференциальных уравнений в частных производных (ЧДУ), постановка краевых задач для ЧДУ, аналитический метод разделения переменных и численный метод конечных разностей. Предполагается, что студенты уже знакомы с обыкновенными дифференциальными уравнениями и прошли обучение работе с пакетом MathCAD.
Данный курс математической физики ориентирован больше на практическое решение задач для ЧДУ. В их решении исключительно важную роль имеют численные методы, т.к. область применения аналитических методов существенно уже. В связи с этим обучение студентов должно происходить с использованием компьютера, и курс создан в виде "живой" книги на языке математического пакета MathCAD, в которой студенты могут изменять числа, писать формулы, видоизменять графики − использовать как уже готовый инструментарий, созданный автором, так и самостоятельно использовать всю мощь программы для решения практических задач. Текст данного курса математической физики является идентичным тексту этого интерфейса, т.е. пособие является копией мультимедийной программы в среде MathCAD: с графикой, гиперсылками, анимацией, "игровой" составляющей – что есть управление визуализацией графики решений задач для ЧДУ. В пособии разобраны примеры решения и даны вопросы и задачи для самостоятельного исследования.
Автор надеется, что использование созданного им мультимедийного инструментария будет способствовать более эффективному практическому обучению решению уравнений математической физики.
